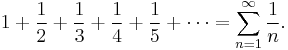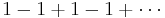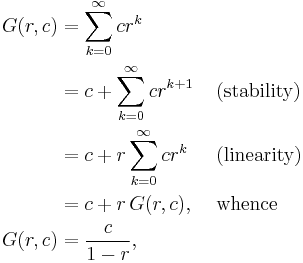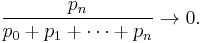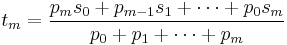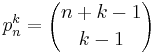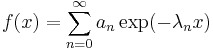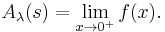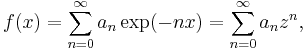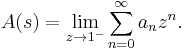Divergent series

In mathematics, a divergent series is an infinite series that is not convergent, meaning that the infinite sequence of the partial sums of the series does not have a limit.

If a series converges, the individual terms of the series must approach zero. Thus any series in which the individual terms do not approach zero diverges. However, convergence is a stronger condition: not all series whose terms approach zero converge. The simplest counterexample is the harmonic series

1 %2B \frac{1}{2} %2B \frac{1}{3} %2B \frac{1}{4} %2B \frac{1}{5} %2B \cdots =\sum_{n=1}^\infty\frac{1}{n}.

The divergence of the harmonic series was proven by the medieval mathematician Nicole Oresme.

In specialized mathematical contexts, values can be usefully assigned to certain series whose sequence of partial sums diverges. A summability method or summation method is a partial function from the set of sequences of partial sums of series to values. For example, Cesàro summation assigns Grandi's divergent series

1 - 1 %2B 1 - 1 %2B \cdots

the value 1/2. Cesàro summation is an averaging method, in that it relies on the arithmetic mean of the sequence of partial sums. Other methods involve analytic continuations of related series. In physics, there are a wide variety of summability methods; these are discussed in greater detail in the article on regularization.

Contents

Theorems on methods for summing divergent series

A summability method M is regular if it agrees with the actual limit on all convergent series. Such a result is called an abelian theorem for M, from the prototypical Abel's theorem. More interesting and in general more subtle are partial converse results, called tauberian theorems, from a prototype proved by Alfred Tauber. Here partial converse means that if M sums the series Σ, and some side-condition holds, then Σ was convergent in the first place; without any side condition such a result would say that M only summed convergent series (making it useless as a summation method for divergent series).

The operator giving the sum of a convergent series is linear, and it follows from the Hahn–Banach theorem that it may be extended to a summation method summing any series with bounded partial sums. This fact is not very useful in practice since there are many such extensions, inconsistent with each other, and also since proving such operators exist requires invoking the axiom of choice or its equivalents, such as Zorn's lemma. They are therefore nonconstructive.

The subject of divergent series, as a domain of mathematical analysis, is primarily concerned with explicit and natural techniques such as Abel summation, Cesàro summation and Borel summation, and their relationships. The advent of Wiener's tauberian theorem marked an epoch in the subject, introducing unexpected connections to Banach algebra methods in Fourier analysis.

Summation of divergent series is also related to extrapolation methods and sequence transformations as numerical techniques. Examples for such techniques are Padé approximants, Levin-type sequence transformations, and order-dependent mappings related to renormalization techniques for large-order perturbation theory in quantum mechanics.

Properties of summation methods

Summation methods usually concentrate on the sequence of partial sums of the series. While this sequence does not converge, we may often find that when we take an average of larger and larger initial terms of the sequence, the average converges, and we can use this average instead of a limit to evaluate the sum of the series. So in evaluating a = a0 + a1 + a2 + ..., we work with the sequence s, where s0 = a0 and sn+1 = sn + an+1. In the convergent case, the sequence s approaches the limit a. A summation method can be seen as a function from a set of sequences of partial sums to values. If A is any summation method assigning values to a set of sequences, we may mechanically translate this to a series-summation method AΣ that assigns the same values to the corresponding series. There are certain properties it is desirable for these methods to possess if they are to arrive at values corresponding to limits and sums, respectively.

  1. Regularity. A summation method is regular if, whenever the sequence s converges to x, A(s) = x. Equivalently, the corresponding series-summation method evaluates AΣ(a) = x.
  2. Linearity. A is linear if it is a linear functional on the sequences where it is defined, so that A(r + s) = A(r) + A(s) and A(ks) = k A(s), for k a scalar (real or complex.) Since the terms an = sn+1 − sn of the series a are linear functionals on the sequence s and vice versa, this is equivalent to AΣ being a linear functional on the terms of the series.
  3. Stability. If s is a sequence starting from s0 and s′ is the sequence obtained by omitting the first value and subtracting it from the rest, so that s′n = sn+1 − s0, then A(s) is defined if and only if A(s′) is defined, and A(s) = s0 + A(s′). Equivalently, whenever a′n = an+1 for all n, then AΣ(a) = a0 + AΣ(a′).

The third condition is less important, and some significant methods, such as Borel summation, do not possess it.

A desirable property for two distinct summation methods A and B to share is consistency: A and B are consistent if for every sequence s to which both assign a value, A(s) = B(s). If two methods are consistent, and one sums more series than the other, the one summing more series is stronger.

There are powerful numerical summation methods that are neither regular nor linear, for instance nonlinear sequence transformations like Levin-type sequence transformations and Padé approximants, as well as the order-dependent mappings of perturbative series based on renormalization techniques.

Axiomatic methods

Taking regularity, linearity and stability as axioms, it is possible to sum many divergent series by elementary algebraic manipulations. For instance, whenever r ≠ 1, the geometric series

\begin{align} G(r,c) & = \sum_{k=0}^\infty cr^k & & \\ & = c %2B \sum_{k=0}^\infty cr^{k%2B1} & & \mbox{ (stability) } \\ & = c %2B r \sum_{k=0}^\infty cr^k & & \mbox{ (linearity) } \\ & = c %2B r \, G(r,c), & & \mbox{ whence } \\ G(r,c) & = \frac{c}{1-r} , & & \\ \end{align}

can be evaluated regardless of convergence. More rigorously, any summation method that possesses these properties and which assigns a finite value to the geometric series must assign this value. However, when r is a real number larger than 1, the partial sums increase without bound, and averaging methods assign a limit of ∞.

Nörlund means

Suppose pn is a sequence of positive terms, starting from p0. Suppose also that

\frac{p_n}{p_0%2Bp_1 %2B \cdots %2B p_n} \rightarrow 0.

If now we transform a sequence s by using p to give weighted means, setting

t_m = \frac{p_m s_0 %2B p_{m-1}s_1 %2B \cdots %2B p_0 s_m}{p_0%2Bp_1%2B\cdots%2Bp_m}

then the limit of tn as n goes to infinity is an average called the Nörlund mean Np(s).

The Nörlund mean is regular, linear, and stable. Moreover, any two Nörlund means are consistent. The most significant of the Nörlund means are the Cesàro sums. Here, if we define the sequence pk by

p_n^k = {n%2Bk-1 \choose k-1}

then the Cesàro sum Ck is defined by Ck(s) = N(pk)(s). Cesàro sums are Nörlund means if k ≥ 0, and hence are regular, linear, stable, and consistent. C0 is ordinary summation, and C1 is ordinary Cesàro summation. Cesàro sums have the property that if h > k, then Ch is stronger than Ck.

Abelian means

Suppose λ = {λ0, λ1, λ2, ...} is a strictly increasing sequence tending towards infinity, and that λ0 ≥ 0. Recall that an = sn+1 − sn is the associated series whose partial sums form the sequence s. Suppose

f(x) = \sum_{n=0}^\infty a_n \exp(-\lambda_n x)

converges for all positive real numbers x. Then the Abelian mean Aλ is defined as

A_\lambda(s) = \lim_{x \rightarrow 0^{%2B}} f(x).

A series of this type is known as a generalized Dirichlet series; in applications to physics, this is known as the method of heat-kernel regularization.

Abelian means are regular, linear, and stable, but not always consistent between different choices of λ. However, some special cases are very important summation methods.

Abel summation

See also: Abel's theorem

If λn = n, then we obtain the method of Abel summation. Here

f(x) = \sum_{n=0}^\infty a_n \exp(-nx) = \sum_{n=0}^\infty a_n z^n,

where z = exp(−x). Then the limit of ƒ(x) as x approaches 0 through positive reals is the limit of the power series for ƒ(z) as z approaches 1 from below through positive reals, and the Abel sum A(s) is defined as

A(s) = \lim_{z \rightarrow 1^{-}} \sum_{n=0}^\infty a_n z^n.

Abel summation is interesting in part because it is consistent with but more powerful than Cesàro summation: A(s) = Ck(s) whenever the latter is defined. The Abel sum is therefore regular, linear, stable, and consistent with Cesàro summation.

Lindelöf summation

If λn = n ln(n), then (indexing from one) we have

f(x) = a_1 %2B a_2 2^{-2x} %2B a_3 3^{-3x} %2B \cdots .

Then L(s), the Lindelöf sum (Volkov 2001), is the limit of ƒ(x) as x goes to zero. The Lindelöf sum is a powerful method when applied to power series among other applications, summing power series in the Mittag-Leffler star.

If g(z) is analytic in a disk around zero, and hence has a Maclaurin series G(z) with a positive radius of convergence, then L(G(z)) = g(z) in the Mittag-Leffler star. Moreover, convergence to g(z) is uniform on compact subsets of the star.

See also

References